Earth Energy Imbalance, the Earth of the Climate Change

Introduction

Black body physic

A black body is a theoretical object absorbing any electromagnetic waves including light. By this process its internal temperature increase. And depending the temperature, the black body will emit electromagnetic waves in new frequency such as at some point the incoming energy will match the emitted energy. This is a theoretical ideal object but it provides very interesting insights on the thermal properties of objects.

Energy flux

Earth can be assimilated to a black body then the properties of the black bodies apply. One of them is the possibility to know the relation between energy emitted and temperature.

$$Q_{emitted} = \sigma T^4$$

$$P_{emitted} = A_{total}\sigma T^4$$

with:

• $Q_{emitted}$ is the flux emitted by Earth in $W \cdot m^{-2}$
• $P_{emitted}$ is the total power dissipated by Earth in $W$
• $\sigma$ is the Stefan–Boltzmann constant ($\sigma = 5{,}67 \cdot 10^{-8} W \cdot m^{−2}\cdot K^{−4}$)
• $T$ is the temperature of the black body in $K$
• $A_{total}$ the total surface of the Earth in $W^{-2}$

Temperature

In the case of the Earth, energy is received from the Sun:

$$P_{received} = A_{projected} Q_{received}$$

In case of thermal equilibrium both flux are equal, then:

$$P_{emited} = P_{received}$$

$$A_{total}\sigma T^4 = A_{projected} Q_{received}$$

$$\frac{A_{total}}{A_{projected}} \sigma T^4 = Q_{received}$$

The total surface is the surface of a sphere, meanwhile the projected surface is the surface of a circle.

$$\frac{A_{total}}{A_{projected}} = \frac{4 \pi r^2}{\pi r^2}$$

$$4 \sigma T^4 = Q_{received}$$

$$T = {^4} \sqrt{{ \frac{Q_{received}}{4 \sigma} }}$$

The constant flux received from the sun is well know thanks to space missions. The top of the atmosphere (TOA) downwelling flux from the Sun is $1361 W.m^{-2}$.

Then the temperature is theoretically: $T = 278{,}32°K = 5{,}16°C$ If the Earth was a perfect black body, then the temperature at the surface would be 5,16°C. Currently the temperature is 15°C (and 16,5°C due to the climate change).

It is important to notice that we talk about a theoretical black body earth in this section. This mean that Earth would absorb and emits radiations in the whole spectrum. The properties of a black body is independent from the wavelengths of the light. Therefore the Earth absorption is not perfect, the albedo is not 0. In the same way, for a black body the emissions is perfect in all the wavelengths (the emissivity $\epsilon$ is equal to 1 on the whole spectrum).

[!TODO]

• Keep the next section ?

An additional result is available at this point :

$$P_{emited} = P_{received}$$

$$A_{total} Q_{emitted} = A_{projected} Q_{received}$$

$$Q_{emitted} = \frac{1}{4} Q_{received}$$

The incident emission is $1361 W.m^{-2}$. This energy is distributed on the Earth surface with the average density of $340{,}25 W.m^{-2}$.

Effect of the the GHGs

The difference between the theoretical black body surface temperature ($5°C$) and the current temperature ($+16°C$) is due to the atmosphere and its greenhouse gas (GHG). The GHG are able to absorb and diffract electromagnetic waves. The surface nature has also an impact on its capacity to absorb the electromagnetic waves. This impact directly the emissivity, absorption, reflection properties of the Earth.

Electromagnetic spectrum

The general equation explaining the relation of the temperature and the emitted wavelengths of a black body is the Planck's law:

$$E_\lambda = \frac{8 \pi h c}{\lambda^5} \frac{1}{e^{\frac{h c}{k T \lambda}} - 1}$$

This law apply to stars provide the next plot. Each line represent a different temperature. The two black lines show limit of the visible light. The Sun temperature is around 5600°K. The maximum of the emissions is in the middle of the visible light band.

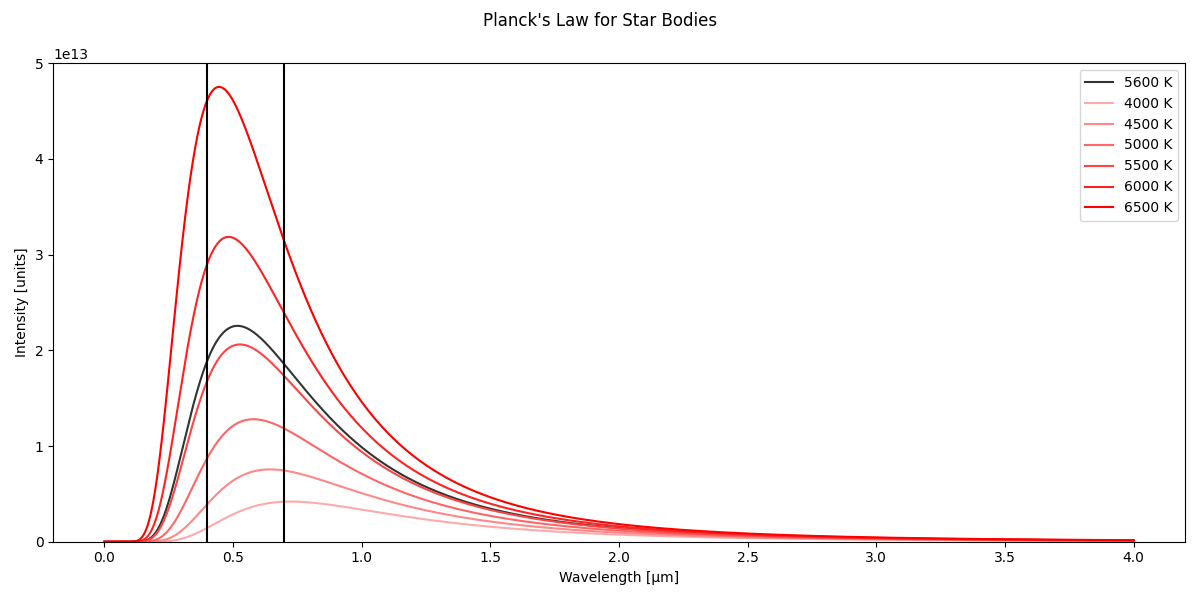
The law can apply to Earth too. In this case we have the next curve.

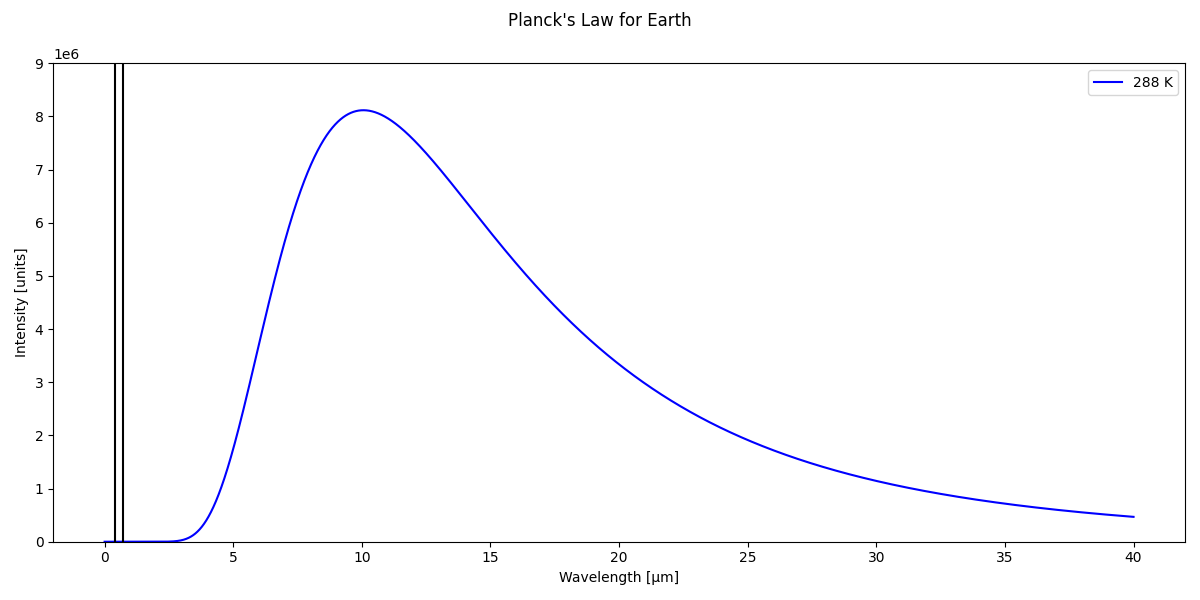
We see the Sun and the Earth does not emit the most of their energy in the same wavelength. Since GHG absorb and diffuse the electromagnetic spectrum on different lengthwave the effect of the GHG will be different on both spectrum. In the case of the Sun we will talk about shortwave radiations and in the case of the Earth it will be longwave radiations. We see also that the Sun is emitting more energy than the Earth. This needs to be corrected by the distance between the Sun and the Earth using the inverse square law:

$${a} = \frac{R_{Sun}^2}{D_{SE}^2}$$

with:

• $a$ the corrective coefficient.
• $R_{Sun}$ the Sun radius.
• $D_{SE}$ the distance between the Sun and Earth

$$a = 2{,}1794 \cdot 10^5$$